Cifrul Cezar
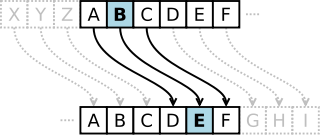
B din textul inițial devine E în textul criptat.În criptografie, cifrul Cezar, numit și cifru de înlocuire, codul lui Cezar sau substituirea Cezarului, este una dintre cele mai simple și mai cunoscute tehnici de criptare. Este un tip de cifru al substituției, în care fiecare literă din textul inițial este înlocuită cu o literă care se află în alfabet la o distanță fixă față de cea înlocuită. De exemplu, cu o deplasare de trei poziții în alfabetul limbii române, A este înlocuit cu D, Ă devine E și așa mai departe. Această metodă este numită așa după Iulius Cezar, care o folosea pentru a comunica cu generalii săi.
Pasul de criptare al cifrului lui Cezar este de obicei încorporat în scheme mai complexe precum Cifrul baka, și încă mai are aplicații moderne în sistemul ROT13. Ca orice alt cifru bazat pe substituții alfabetice, cifrul lui Cezar este simplu de descifrat și în practică nu oferă securitate suficientă.
Exemplu
[modificare | modificare sursă]Transformarea poate fi reprezentată printr-o aliniere a două alfabete; alfabetul cifrului este alfabetului normal rotat la stânga sau la dreapta cu un număr de poziții. În exemplul de mai jos cifrul folosește o rotație la stânga cu cinci poziții (parametrul de deplasare, aici 5, este folosit drept cheia cifrării):
Normal: AĂÂBCDEFGHIÎJKLMNOPQRSȘTȚUVWXYZCifru : DEFGHIÎJKLMNOPQRSȘTȚUVWXYZAĂÂBC
Pentru a cripta un mesaj se caută fiecare literă a mesajului în linia "Normal" și se scrie litera corespunzătoare din linia "Cifru". Pentru decriptarea unui text cifrat se procedează invers.
Mesaj inițial: ANA ARE MERE DE LA BUNICA SAMesaj criptat: DSD DUÎ RÎUÎ IÎ QD GZSMHD VD
Criptarea după cifrul Cezar poate fi reprezentată folosind aritmetică modulară prin transformarea literelor în numere conform schemei A = 0, Ă = 1,..., Z = 30[1]. Astfel, alfabetul devine o secvență de 31 de numere, iar criptarea unei litere cu poziția din alfabet printr-o deplasare spre dreapta cu n poziții poate fi descrisă matematic ca[2]
Decriptarea este făcută similar:
(Există mai multe definiții pentru operația modulo. În operația de mai sus, rezultatul se află în intervalul 0...30. Dacă x+n sau x-n nu se află în intervalul 0...30, atunci prin operația modulo se scad sau se adună 31 de atâtea ori până când condiția este îndeplinită).
Metoda de înlocuire este aceeași pe întreg parcursul mesajului, de aceea cifrul este clasificat ca un tip de substituție monoalfabetică, spre deosebire de substituția polialfabetică.
Istorie și utilizare
[modificare | modificare sursă]
Cifrul Cezar este denumit după Iulius Cezar, care, conform Suetoniu, îl folosea cu o deplasare de 3 pentru protejarea mesajelor cu importanță militară:
- Dacă avea ceva confidențial de comunicat, scria încifrat, adică schimba ordinea literelor din alfabet, astfel încât nu se putea înțelege nici un cuvânt. Dacă cineva dorește să descifreze și să înțeleagă, trebuie să înlocuiască a patra literă din alfabet, adică D, cu A, și așa mai departe pentru celelalte. — Suetoniu, Viața lui Iulius Cezar 56 [1] Arhivat în , la Wayback Machine..
Deși Cezar a fost primul care a fost folosit cifrul într-un mod în care se poate atesta, alte cifruri bazate pe substituție se cunosc ca fiind folosite anterior. Nepotul lui Iulius Cezar, Augustus, a folosit de asemenea cifrul, dar cu o deplasare de unu:
- Când scria încifrat, scria B în loc de A, C în loc de B, și restul literelor pe același principiu, folosind AA pentru X. — Suetoniu, Viața lui Augustus 88.
Există dovezi cum că Iulius Cezar folosea și sisteme mai complicate[3], iar un scriitor, Aulus Gellius, referă un tratat (acum pierdut) despre cifrurile lui:
- Există chiar și un tratat scris în mod ingenios de către gramaticianul Probus cu privire la semnificația secretă a literelor din compoziția epistolelor lui Cezar. — Aulus Gellius, 17.9.1–5.
Nu se știe cât de util era cifrul Cezar în acel timp, dar este probabil ca el să fie destul de sigur, atât timp cât numai câțiva dintre inamicii lui Cezar erau în stare să scrie și să citească, dar mai ales să cunoască concepte de criptanaliză[4]. Presupunând că un atacator reușea să citească un mesaj, nu există indicii cu privire la existența unor tehnici de soluționare a cifrurilor cu substituție. Primele dovezi cunoscute sunt lucrările din secolul al IX-lea ale lui Al-Kindi, în lumea arabă, o dată cu descoperirea analizei frecvenței[5].
Un cifru Cezar cu deplasarea de o unitate a fost utilizat la încifrarea numelor lui Dumnezeu pe spatele Mezuzelor. Acest fapt poate fi o rămășiță din vremurile în care evreilor nu le era permis să dețină Mezuze. Înseși literele criptogramei conțin un nume divin, despre care se considera că ține forțele răului la distanță[6].
În secolul al XIX-lea, secțiunea de anunțuri personale din ziare era folosită pentru schimbarea de mesaje criptate folosind scheme simple de încifrare. Kahn (1967) descrie exemple de îndrăgostiți care comunicau secret folosind cifrul Cezar în The Times[7]. Chiar și în 1915, cifrul Cezar a fost folosit de armata rusească ca înlocuitor pentru cifruri mai complicate care s-au dovedit a fi prea dificile pentru ca trupele lor să le folosească; criptanaliștii germani și austrieci nu aveau nici o dificultate în decriptarea mesajelor lor[8].
Cifrurile Cezar pot fi găsite astăzi în jucăriile pentru copii. O deplasare de 13 este efectuată în algoritmul ROT13, o metodă simplă de alambicare a textului de pe unele forumuri de pe Internet, dar nu ca metodă de criptare[9].
Cifrul Vigenère folosește un cifru Cezar cu o deplasare diferită la fiecare poziție din text; valoarea deplasării este definită folosind un cuvânt-cheie care se repetă. Dacă o cheie este la fel de lungă ca și mesajul și aleasă aleatoriu, atunci acesta este un cifru care nu poate fi spart atât timp cât cheia este secretă. Cuvintele cheie mai scurte decât mesajul introduc un șablon ciclic care poate fi detectat cu o versiune statistică avansată a analizei frecvenței[10].
În aprilie 2006, capul mafiot evadat Bernardo Provenzano a fost capturat în Sicilia parțial datorită criptanalizei mesajelor sale scrise într-o variantă a cifrului Cezar. Cifrul lui Provenzano folosea numere, astfel încât „A” era scris ca „4”, „B” ca „5” ș.a.m.d.[11]
Spargerea cifrului
[modificare | modificare sursă]| Deplasare în decriptare | Text candidat |
|---|---|
| 0 | dxdhjșuydx
|
| 1 | cwcgîsțxcw
|
| 2 | bvbfirtwbv
|
| 3 | âuâehqșvâu
|
| 4 | ățădgpsuăț
|
| 5 | atacforțat
|
| 6 | zșzbenqtzș
|
| 7 | ysyâdmpșys
|
| ... | |
| 28 | gagjmuxăga
|
| 29 | fzfîlțwafz
|
| 30 | eyeiktvzey
|
Cifrul Cezar poate fi spart ușor chiar și având la dispoziție numai criptotextul. Două situații pot fi luate în considerare:
- atacatorul cunoaște (sau ghicește) că a fost folosită un fel de substituție simplă, dar nu neapărat o schemă Cezar
- atacatorul știe că s-a folosit cifrul Cezar, dar nu cunoaște valoarea de deplasare.
În primul caz, cifrul poate fi spart folosind aceeași tehnică ca pentru cazul general de substituție simplă, precum analiza frecvenței sau cuvinte șablon[12]. În timpul decriptării, este foarte probabil ca atacatorul să observe regularitatea în soluție și să deducă că cifrul Cezar este algoritmul folosit.

În al doilea caz, spargerea schemei este mult mai simplă. Deoarece numărul de deplasări posibile e limitat (31 în română), fiecare din ele poate fi testată printr-un atac prin forță brută[14]. O cale de a realiza acest lucru este de a scrie un fișier cu criptotextul într-un tabel cu toate deplasările posibile[15] — tehnică numită uneori „completarea componentei normale”[16]. Exemplul este dat pentru criptotextul „DXDHJȘUYDX”. Textul normal este imediat recognoscibil de ochi la valoarea 5. O altă cale de a vizualiza această metodă este de a scrie sub fiecare literă alfabetul înapoi față de literă. Acest atac poate fi accelerat folosind șiruri cu alfabetul scris invers. Șirurile sunt apoi aliniate astfel încât criptotextul să apară pe un rând, iar astfel textul inițial va apărea pe un alt rând.
O altă abordare a atacului prin forță brută este identificarea literelor conform distribuției lor în limba în care a fost scris textul. Prin crearea graficului frecvențelor literelor din criptotext și prin cunoașterea distribuției obișnuite, un om poate descoperi valoarea deplasării prin observarea decalajului dintre anumite caracteristici ale graficului. Aceasta este cunoscută ca analiza frecvenței[17]. Și computerele pot determina acest lucru prin măsurarea echivalenței dintre distribuția curentă și distribuția așteptată; de exemplu, poate fi utilizat testul chi-pătrat[18].
Pentru texte naturale va exista doar o decriptare plauzibilă, deși pentru texte normale foarte scurte se poate să existe mai multe versiuni. De exemplu, criptotextul „UHU” poate, în mod plauzibil, să fie decriptat în „ana” sau în „bob”; similar, „PR” în „ac” sau „ce”.
Criptări și decriptări multiple nu aduc nimic în plus în ceea ce privește securitatea. Aceasta pentru că două criptări, de exemplu deplasarea A și deplasarea B, vor fi echivalente cu deplasarea A + B. În termeni matematici, criptarea cu diferite chei formează un grup[19].
Referințe
[modificare | modificare sursă]- ^ Luciano, Dennis; Gordon Prichett (). „Cryptology: From Caesar Ciphers to Public-Key Cryptosystems”. The College Mathematics Journal. 18 (1): 3.
- ^ Wobst, Reinhard (). Cryptology Unlocked. Wiley. p. 19. ISBN 978-0470060643.
- ^ Reinke, Edgar C. (). „Classical Cryptography”. The Classical Journal. 58 (3): 114.
- ^ Pieprzyk, Josef; Thomas Hardjono; Jennifer Seberry (). Fundamentals of Computer Security. Springer. pp. p.6. ISBN 3540431012.
- ^ Singh, Simon (). The Code Book. Anchor. pp. pp.14–20. ISBN 0385495323.
- ^ Alexander Poltorak. „Mezuzah and Astrology”. chabad.org. Accesat în .
- ^ Kahn, David (). The Codebreakers. pp. pp.775–6. ISBN 978-0-684-83130-5.
- ^ Kahn, David (). The Codebreakers. pp. pp.631–2. ISBN 978-0-684-83130-5.
- ^ Wobst, Reinhard (). Cryptology Unlocked. Wiley. p. 20. ISBN 978-0470060643.
- ^ Kahn, David (). The Codebreakers. ISBN 978-0-684-83130-5.
- ^ en "Mafia boss undone by clumsy crypto" The Register
- ^ Beutelspacher, Albrecht (). Cryptology. Mathematical Association of America. pp. pp.9–11. ISBN 0-88385-504-6.
- ^ Vlad, Adriana; Mitrea Adrian; Mitrea, Mihai (). Two Frequency-rank Laws for Letters in Printed Romanian (PDF). SEPLN. pp. 153–160. Accesat în .
- ^ Beutelspacher, Albrecht (). Cryptology. Mathematical Association of America. pp. pp.8–9. ISBN 0-88385-504-6.
- ^ Leighton, Albert C. (). „Secret Communication among the Greeks and Romans”. Technology and Culture. 10 (2): 153.
- ^ Sinkov, Abraham; Paul L. Irwin (). Elementary Cryptanalysis: A Mathematical Approach. Mathematical Association of America. pp. pp.13–15. ISBN 0883856220.
- ^ Singh, Simon (). The Code Book. Anchor. pp. pp.72–77. ISBN 0385495323.
- ^ Savarese, Chris; Brian Hart (). „The Caesar Cipher”. Accesat în .
- ^ Wobst, Reinhard (). Cryptology Unlocked. Wiley. p. 31. ISBN 978-0470060643.
Bibliografie
[modificare | modificare sursă]- David Kahn, The Codebreakers — The Story of Secret Writing, 1967. ISBN 0-684-83130-9.
- F.L. Bauer, Decrypted Secrets, ediția a doua, 2000, Springer. ISBN 3-540-66871-3.
- Chris Savarese and Brian Hart, Cifrul Cezar, 1999
Legături externe
[modificare | modificare sursă]Criptografie clasică
|
|---|
| Cifruri: ADFGVX | Afin | Alberti | Atbash | Autocheie | Bifid | Carte | Cezar | Cod Smithy | Codul bătăilor | Cuvânt cheie | Două pătrate | Francmasonic | Hill | Nihilist | Patru pătrate | Permutare | Playfair | Polialfabetic | Polybius | Rail Fence | Reihenschieber | Reservehandverfahren | ROT13 | Running key | Schitală | Solitaire | Straddling checkerboard | Substituție | Transpoziție | Trifid | VIC | Vigenère |
| Criptanaliză: Analiza frecvenței | Index de coincidență |
| Diverse: Criptogramă | Bacon | Pătratul lui Polybius | Schitală | Straddling checkerboard | Tabula recta |
| Istoria criptologiei | Criptanaliză | Portalul criptografiei | Subiecte în criptografie |
| Algoritm cu chei simetrice | Cifru bloc | Cifru stream | Criptografie cu chei publice | Funcție hash criptografică | Cod de autentificare a mesajelor | Număr aleatoriu |



