120-celule icosaedric
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
| 120-celule icosaedric | |
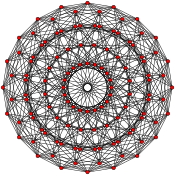
 Proiecție ortogonală | |
| Tip | Politop Schläfli–Hess |
|---|---|
| Simbol Schläfli | {3,5,5/2} |
| Diagramă Coxeter | |
| Celule | 120 {3,5}  |
| Fețe | 1200 {3} |
| Laturi | 720 |
| Vârfuri | 120 |
| Figura vârfului |  {5,5/2} |
| Grup Coxeter | H4, [3,3,5] |
| Dual | micul 120-celule stelat |
| Proprietăți | regulat |
În geometrie 120-celule icosaedric sau icosaplexul este un politop cvadridimensional stelat regulat. Cele 120 de celule ale sale sunt icosaedre. Are 120 de vârfuri, 720 de laturi și 1200 de fețe. Are simbolul Schläfli {3,5,5/2}. Este unul dintre cele 10 politopuri Schläfli–Hess regulate.
Este construit de 5 icosaedre în jurul fiecărei laturi, formând o figură pentagramică. Figura vârfului este marele dodecaedru.
Politopuri înrudite
[modificare | modificare sursă]Are același aranjament al laturilor ca și 600-celule, marele 120-celule și largul 120-celule și are în comun cele 120 de vârfuri cu toate celelalte politopuri Schläfli–Hess, cu excepția marelui larg 120-celule stelat (altă stelare a 120-celule).
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
Ca 600-celule fațetat, înlocuind celulele simpliciale ale 600-celule cu celule icosaedrice de politop pentagonal, ar putea fi văzut ca un analog cvadridimensional al marelui dodecaedru, în care se înlocuiesc fețele triunghiulare ale icosaedrului cu fețe pentagonale. 120-celule icosaedric este dual cu micul 120-celule stelat, care ar putea fi considerat un analog cvadridimensional al micului dodecaedru stelat, dual de marele dodecaedru. Cu dualul său poate forma compusul de 120-celule icosaedric și micul 120-celule stelat.
Bibliografie
[modificare | modificare sursă]- de Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1].
- en H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN: 0-486-61480-8.
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26, Regular Star-polytopes, pp. 404–408)
- en Klitzing, Richard. „4D uniform polytopes (polychora) o3o5o5/2o - fix”.
Vezi și
[modificare | modificare sursă]- 4-politopuri convexe regulate - Mulțimea 4-politopurilor convexe regulate
- Poliedre Kepler–Poinsot – poliedre stelate regulate
- Poligon stelat – poligoane stelate regulate
Legături externe
[modificare | modificare sursă]- en Regular polychora Arhivat în , la Wayback Machine.
- en Discussion on names
- de Reguläre Polytope
- en The Regular Star Polychora

