Rețea Hopfield
O rețea Hopfield (sau memorie asociativă) este o formă de rețea neurală recurentă care poate servi ca memorie adresabilă prin conținut. Rețelele Hopfield, numite după John Hopfield, constau dintr-un singur strat de neuroni, în care fiecare neuron este conectat la toți ceilalți, nu și la el însuși. Aceste conexiuni sunt bidirecționale și simetrice, ceea ce înseamnă că ponderea conexiunii de la neuronul i la neuronul j este aceeași cu ponderea celei de la neuronul j la neuronul i. Șabloanele pot fi invocate asociativ prin fixarea anumitor intrări, care împing rețeaua să evolueze dinamic în sensul minimizării unei funcții energetice, către stăride energie minimă local care corespund șabloanelor stocate. Șabloanele sunt învățate asociativ (sau „stocate”) printr-un algoritm de învățare Hebbian.
Una dintre caracteristicile cheie ale rețelelor Hopfield este capacitatea lor de a readuce modele complete din intrări parțiale sau afectate de zgomote, făcându-le să fie robuste în fața datelor incomplete sau corupte. Legătura lor cu mecanica statistică, rețelele recurente și psihologia cognitivă umană a dus la aplicarea lor în diferite domenii, inclusiv fizică, psihologie, neuroștiințe și teoria și practica învățării automate.
Istorie
[modificare | modificare sursă]O origine a conceptului de memorie asociativă este psihologia cognitivă, anume conceptul denumit la fel în acel domeniu. Frank Rosenblatt a studiat „perceptronii cuplati încrucișat în buclă închisă”, care sunt rețele de perceptroni cu 3 straturi al căror strat mijlociu conține conexiuni recurente care se modifică după o regulă de învățare hebbiană.[1](pp73-75)[2](Chapter 19, 21) Karl Steinbuch, care dorea să înțeleagă procesul de învățare, și inspirat de copiii săi pe care îi urmărea învățând,[3] a publicat Lernmatrix în 1961.[4][5]
Cercetări similare au fost efectuate cu corelograma lui (DJ Willshaw et al., 1969).[6] În ( Kohonen, 1974)[7] o memorie asociativă a fost antrenată prin coborâre de gradient.

O altă origine a memoriei asociative a fost mecanica statistică. Modelul Ising a fost publicat în anii 1920 ca model de magnetism, dar studia echilibrul termic, care nu se modifică în timp. Roy J. Glauber a studiat în 1963 modelul Ising care evoluează în timp, ca proces ce conduce la echilibru termic (dinamica Glauber), adăugând componenta timp.[8]
A doua componentă care a fost adăugată a fost adaptarea la stimuli. Descriind fenomenul independent, Kaoru Nakano în 1971[9][10] și Shun'ichi Amari în 1972 au propus modificarea ponderilor unui model Ising prin regula de învățare hebbiană ca model de memorie asociativă.[11] Aceeași idee a fost publicată de William A. Little(de)[traduceți] în 1974,[12] care a fost recunoscut de Hopfield în lucrarea sa din 1982.
Vezi Carpenter (1989)[13] pentru o descriere tehnică a unora dintre aceste prime lucrări în domeniul memoriilor asociative.
Modelul Sherrington–Kirkpatrick, publicat în 1975, [14] este o rețea Hopfield cu inițializare aleatorie. Sherrington și Kirkpatrick au descoperit că este foarte probabil ca funcția energetică a modelului SK să aibă multe minime locale. În lucrarea din 1982, Hopfield a aplicat această teorie recent dezvoltată pentru a studia rețelele Hopfield cu funcții de activare binară.[15] Într-o lucrare din 1984, el a extins aceasta la funcțiile de activare continuă,[16] extensie care a devenit un model standard pentru studiul rețelelor neurale prin mecanica statistică.[17][18]
Un progres major în capacitatea de stocare a memoriilor a fost dezvoltat de Krotov și Hopfield în 2016[19] printr-o schimbare a dinamicii rețelei și a funcției energetice. Această idee a fost extinsă în continuare de Demircigil și colaboratorii în 2017.[20] Dinamica continuă a modelelor cu capacitate mare de memorie a fost dezvoltată într-o serie de lucrări între 2016 și 2020.[19][21][22] Memorii asociative Hopfield cu mare capacitate de stocare se numesc acum memorii dens asociative sau rețele Hopfield moderne.
În 2024, John J. Hopfield și Geoffrey E. Hinton au primit Premiul Nobel pentru Fizică pentru contribuțiile lor fundamentale la învățarea automată, cum ar fi rețeaua Hopfield.
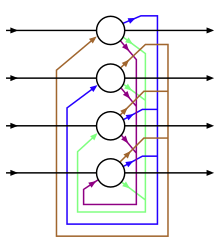
Unitățile din rețele Hopfield sunt unități cu prag binar, adică unitățile iau doar două valori diferite pentru stările lor, iar valoarea este stabilită prin verificarea dacă intrarea unității îi depășește sau nu pragul . Rețelele Hopfield discrete descriu relațiile dintre neuronii binari (activi sau nu). .[15] La un anumit moment, starea rețelei neuronale este descrisă de un vector , care înregistrează ce neuroni se declanșează într-un cuvânt binar de biți.
Interacțiunile între neuroni au unități care, de obicei, iau valori de 1 sau -1, iar această convenție va fi folosită pe tot parcursul acestui articol. Cu toate acestea, altă literatură ar putea folosi unități care iau valori de 0 și 1. Aceste interacțiuni sunt „învățate” prin legea de asociere a lui Hebb, astfel încât, pentru o anumită stare și pentru două noduri distincte
dar .
Regula de învățare hebbiană ia forma când unitățile își asumă valori în .
Odată ce rețeaua este antrenată, nu mai evoluează. Dacă în rețeaua neurală se introduce o nouă stare a neuronilor , rețeaua acționează asupra neuronilor astfel încât
- dacă
- dacă
unde este valoarea de prag a celui de-al i-lea neuron (deseori considerată 0).[23] În acest fel, rețelele Hopfield au capacitatea de a „reține” stările stocate în matricea de interacțiuni, deoarece dacă o stare nouă este supusă matricei de interacțiuni, fiecare neuron se va schimba până când se potrivește cu starea inițială (vezi secțiunea Rețea Hopfield § #Actualizare de mai jos).
Conexiunile într-o rețea Hopfield au de obicei următoarele restricții:
- (nicio unitate nu are o legătură cu ea însăși)
- (conexiunile sunt simetrice)
Constrângerea conform căreia ponderile sunt simetrice garantează că funcția de energie scade monoton, respectând regulile de activare.[24] O rețea cu ponderi asimetrice poate prezenta un comportament periodic sau haotic; cu toate acestea, Hopfield a descoperit că acest comportament este limitat la părți relativ mici ale spațiului de fază și nu afectează capacitatea rețelei de a acționa ca un sistem de memorie asociativă adresabil prin conținut.
Hopfield a modelat și rețele neurale pentru valori continuale, în care producția electrică a fiecărui neuron nu este binară, ci o valoare între 0 și 1.[16] El a descoperit că și acest tip de rețea este capabil să stocheze și să reproducă stări memorate.
Fiecare pereche de unități i și j dintr-o rețea Hopfield are o conexiune care este descrisă de greutatea conectivității . În acest sens, rețeaua Hopfield poate fi descrisă formal ca un graf neorientat complet , unde este o mulțime de neuroni McCulloch–Pitts și este o funcție care leagă perechi de unități la o valoare reală, ponderea conectivității.
Actualizare
[modificare | modificare sursă]Actualizarea unei unități (nodul din graf care simulează neuronul artificial) în rețeaua Hopfield se realizează folosind următoarea regulă:
Capacitatea de stocare poate fi dată ca unde este numărul de neuroni din rețea.
- este ponderea conexiunii de la unitatea j la unitatea i.
- este starea unității i.
- este pragul unității i.
Actualizările în rețeaua Hopfield pot fi efectuate în două moduri diferite:
- Asincron: Unitățile sunt actualizate una câte una. Unitatea de actualizat poate fi aleasă la întâmplare sau poate fi impusă o ordine predefinită încă de la început.
- Sincron: Toate unitățile sunt actualizate în același timp. Aceasta necesită un ceas central al sistemului pentru a menține sincronizarea. Această metodă este văzută de unii ca fiind mai puțin realistă, bazată pe faptul că sistemele biologice și sistemele fizice de interes nu au un ceas global observat.
Neuronii „se atrag sau se resping reciproc” în spațiul stărilor
[modificare | modificare sursă]Ponderea legăturii dintre două unități are un impact puternic asupra valorilor neuronilor. Fie ponderea conexiunii între doi neuroni i și j. Dacă , regula de actualizare înseamnă că:
- atunci când , contribuția lui j în suma ponderată este pozitivă. Astfel, este tras de j spre valoarea
- când , contribuția lui j în suma ponderată este negativă. Din nou, este împins de j către valoarea
Astfel, valorile neuronilor i și j vor converge dacă ponderea legăturii dintre ei este pozitivă. Similar, ei vor diverge dacă ponderea este negativă.
Proprietăți de convergență ale rețelelor Hopfield discrete și continue
[modificare | modificare sursă]În lucrarea sa din 1990,[25] Bruck a studiat rețelele Hopfield discrete și a demonstrat o teoremă de convergență generalizată care se bazează pe conexiunea dintre dinamica rețelei și tăieturile din graful asociat. Această generalizare a acoperit atât dinamica asincronă, cât și cea sincronă și a prezentat dovezi elementare bazate pe algoritmi greedy pentru tăietura maximă în grafuri. O lucrare ulterioară[26] a cercetat mai departe comportamentul oricărui neuron atât în rețele Hopfield în timp discret, cât și în timp continuu, atunci când funcția energetică corespunzătoare este minimizată în timpul unui proces de optimizare. Bruck arată[25] că neuronul j își schimbă starea dacă și numai dacă scade și mai mult următoarea pseudo-tăietură polarizată. Rețeaua Hopfield discretă minimizează următoarea pseudo-tăietură polarizată[26] pentru matricea de ponderi sinaptice ale rețelei Hopfield.
unde:
Rețeaua Hopfield în timp discret minimizează întotdeauna exact următoarea pseudo-tăietură:[25][26]
Rețeaua Hopfield în timp continuu minimizează întotdeauna o limită superioară la următoarea tăietură ponderată:[26]
unde este o funcție sigmoidă centrată în zero.
Rețeaua Hopfield complexă tinde, pe de altă parte, în general să minimizeze așa-numita tăietură-umbră a matricei complexe de ponderi a rețelei.[27]
Energie
[modificare | modificare sursă]
Rețelele Hopfield au o valoare scalară asociată cu fiecare stare a rețelei, denumită „energia”, E, a rețelei, unde:
Această cantitate se numește „energie” deoarece fie scade, fie rămâne aceeași la actualizarea unităților de rețea. Mai mult, în cazul actualizării repetate, rețeaua va converge în cele din urmă către o stare care este un minim local în funcția de energie (care este considerată a fi o funcție Leapunov).[15] Astfel, dacă o stare este un minim local în funcția de energie, atunci este o stare stabilă a rețelei. Această funcție energetică aparține unei clase generale de modele din fizică care poartă denumirea de modele Ising; acestea, la rândul lor, sunt un caz special de rețele Markov, deoarece măsura de probabilitate asociată, măsura Gibbs, are proprietatea Markov.
Rețelele Hopfield în optimizare
[modificare | modificare sursă]Hopfield și Tank au prezentat aplicația rețelelor Hopfield în rezolvarea clasicei probleme a comis-voiajorului în 1985.[28] De atunci, rețeaua Hopfield a fost utilizată pe scară largă pentru optimizare. Ideea utilizării rețelei Hopfield în probleme de optimizare este simplă: dacă se poate scrie o funcție de cost cu sau fără constrângeri poate fi scrisă sub forma unei funcții E de energie Hopfield, atunci există o rețea Hopfield ale cărei puncte de echilibru reprezintă soluții la problema de optimizare cu sau fără constrângeri. Minimizarea funcției de energie Hopfield minimizează și funcția obiectiv, dar satisface și constrângerile, deoarece constrângerile sunt „încorporate” în ponderile sinaptice ale rețelei. Deși cea mai bună metodă de includere a constrângerilor de optimizare în ponderile sinaptice rămâne o sarcină provocatoare, multe probleme dificile de optimizare cu constrângeri în diferite discipline au fost convertite la funcția de energie Hopfield: sisteme de memorie asociativă, conversie analog-digitală, probleme de alocări de taskuri, alocare pătratică și alte probleme NP-complete asociate, problema alocării canalelor în rețelele fără fir, problema rutării într-o rețela mobilă ad-hoc, restaurarea imaginilor, identificarea sistemelor, optimizarea combinatorică etc. Cu toate acestea, deși este posibilă convertirea problemelor de optimizare dificile la funcții energetice Hopfield, aceasta nu garantează convergența către o soluție (nici măcar tot în timp exponențial).[29]
Inițializare și rulare
[modificare | modificare sursă]Inițializarea rețelelor Hopfield se face prin setarea valorilor unităților la modelul de pornire dorit. După aceea se efectuează actualizări repetate până când rețeaua converge către un șablon atractor. Convergența este în general asigurată, deoarece Hopfield a demonstrat că atractorii acestui sistem dinamic neliniar sunt stabili, nu periodici sau haotici ca în alte sisteme. Prin urmare, în contextul rețelelor Hopfield, un șablon de atracție este o stare finală stabilă, un șablon care nu-și poate schimba nicio valoare în cursul actualizării.
Antrenarea
[modificare | modificare sursă]Antrenarea unei rețele Hopfield presupune scăderea energiei stărilor pe care rețeaua ar trebui să le „memoreze”. Aceasta permite rețelei să servească drept sistem de memorie adresabilă prin conținut, adică rețeaua va converge către o stare „memorată” dacă i se dă doar o parte din stare. Rețeaua poate fi folosită pentru a reveni de la o intrare distorsionată la starea antrenată care este cea mai asemănătoare cu acea intrare. Aceasta se numește memorie asociativă deoarece recuperează amintirile pe baza asemănării. De exemplu, dacă antrenăm o rețea Hopfield cu cinci unități astfel încât starea (1, −1, 1, −1, 1) să fie un minim de energie și dăm rețelei starea (1, −1, −1, −1, 1), ea va converge către (1, −1, 1, −1, 1). Astfel, rețeaua este antrenată corespunzător atunci când energia stărilor pe care rețeaua ar trebui să le memoreze sunt minime locale. Spre deosebire de antrenarea cu Perceptron, pragurile neuronilor nu sunt niciodată actualizate.
Reguli de învățare
[modificare | modificare sursă]Există diferite reguli de învățare care pot fi folosite pentru a stoca informații în memoria rețelei Hopfield. Este de dorit ca o regulă de învățare să aibă ambele dintre următoarele două proprietăți:
- Locală: o regulă de învățare este locală dacă fiecare pondere este actualizată folosind informațiile disponibile neuronilor de ambele părți ale conexiunii care este asociată cu acea pondere particulară.
- Incrementală: noi șabloane pot fi învățate fără a utiliza informații din vechile șabloane care au fost folosite și pentru antrenament. Adică, atunci când un model nou este folosit pentru antrenament, noile valori pentru ponderi depind doar de valorile vechi și de noul model.[30]
Aceste proprietăți sunt de dorit, deoarece o regulă de învățare care le satisface este mai plauzibilă din punct de vedere biologic. De exemplu, deoarece creierul uman învață mereu concepte noi, se poate argumenta că învățarea umană este incrementală. Un sistem de învățare care nu era incremental ar fi, în general, antrenat o singură dată, cu un lot uriaș de date de instruire.
Regula de învățare hebbiană pentru rețelele Hopfield
[modificare | modificare sursă]Teoria Hebbiană a fost introdusă de Donald Hebb în 1949 pentru a explica „învățarea asociativă”, în care activarea simultană a celulelor neuronale duce la creșteri pronunțate ale forței sinaptice între acele celule.[31] Este adesea rezumată prin fraza: „Neuronii care se declanșează împreună se conectează împreună. Neuronii care se declanșează desincronizat nu se pot lega”.
Regula hebbiană este atât locală, cât și incrementală. Pentru rețelele Hopfield, este implementată în următoarea manieră atunci când se învață șabloane binare:
unde reprezintă bitul i din șablonul .
Dacă biții corespunzători neuronilor i și j sunt egali în șablonul , apoi produsul va fi pozitiv. Aceasta ar avea, la rândul său, un efect pozitiv asupra ponderii iar valorile lui i și j vor tinde să devină egale. Dacă biții corespunzători neuronilor i și j sunt diferiți, atunci se întâmplă opusul.
Regula de învățare Storkey
[modificare | modificare sursă]Această regulă a fost introdusă de Amos Storkey în 1997 și este atât locală, cât și incrementală. Storkey a arătat și că o rețea Hopfield antrenată folosind această regulă are o capacitate mai mare decât o rețea corespunzătoare antrenată folosind regula hebbiană.[32] Se spune că matricea de ponderi a unei rețele neurale atractoare urmează regula de învățare Storkey dacă respectă condiția:
unde este o formă de corp local[30] la neuronul i.
Această regulă de învățare este locală, deoarece sinapsele iau în considerare doar neuronii de la capetele lor. Regula utilizează mai multă informație din șabloane și ponderi decât regula hebbiană generalizată, datorită efectului corpului local.
Șabloane false
[modificare | modificare sursă]Șabloanele pe care rețeaua le folosește pentru antrenament (numite stări de recuperare) devin atractori ai sistemului. Actualizările repetate ar duce în cele din urmă la convergența către una dintre stările de recuperare. Cu toate acestea, uneori rețeaua va converge către șabloane false (diferite de șabloanele de antrenare).[33] De fapt, numărul de șabloane false poate fi exponențial în raport cu numărul de șabloane stocate, chiar dacă șabloanele stocate sunt ortogonale.[34] Energia din aceste șabloane false este și ea un minim local. Pentru fiecare șablon stocat x, negația -x este și ea un șablon fals.
O stare falsă poate fi și o combinație liniară a unui număr impar de stări de recuperare. De exemplu, când se folosesc 3 șabloane , se poate obține următoarea stare falsă:
Nu pot exista șabloane false cu un număr par de stări, deoarece ele ar putea avea suma zero.[33]
Capacitate
[modificare | modificare sursă]Capacitatea rețelei în modelul de rețea Hopfield este determinată de cantitățile de neuroni și conexiunile dintr-o rețea dată. Prin urmare, numărul de amintiri care pot fi stocate depinde de neuroni și conexiuni. Mai mult, s-a demonstrat că precizia de reamintire între vectori și noduri a fost de 0,138 (aproximativ 138 de vectori pot fi recuperați din stocare pentru fiecare 1000 de noduri) (Hertz și colab., 1991). Prin urmare, este evident că vor apărea multe greșeli dacă se încearcă stocarea unui număr mare de vectori. Atunci când modelul Hopfield nu reamintește modelul corect, este posibil să fi avut loc o intruziune, deoarece elementele legate semantic tind să deruteze individul și are loc reamintirea modelului greșit. Prin urmare, se arată că modelul de rețea Hopfield confundă un articol stocat cu un altul la recuperare. Amintirile perfecte și capacitatea mare, >0,14, pot fi încărcate în rețea prin metoda de învățare Storkey. Ulterior, modelele inspirate de rețeaua Hopfield au fost concepute pentru a crește limita de stocare și pentru a reduce rata de eroare de recuperare, unele fiind capabile de învățare într-un singur pas.[35]
Rețelele Hopfield sunt un model pentru învățarea asociativă și procesul uman al amintirilor.[36][37] Ele țin cont de memoria asociativă prin încorporarea vectorilor de memorie. Vectorii de memorie pot fi utilizați ușor, iar acest lucru ar declanșa regăsirea celui mai asemănător vector din rețea. Totuși, din cauza acestui proces pot apărea intruziuni. În memoria asociativă pentru rețelele Hopfield, există două tipuri de operații: auto-asociere și hetero-asociere. Prima fiind atunci când un vector este asociat cu el însuși, iar ultima fiind atunci când doi vectori diferiți sunt asociați la stocare. Mai mult, ambele tipuri de operații pot fi stocate într-o singură matrice de memorie, dar numai dacă acea matrice de reprezentare dată nu este una sau alta dintre operații, ci mai degrabă combinația (auto-asociativă și hetero-asociativă) a celor două.
Modelul rețelelor Hopfield utilizează aceeași regulă de învățare ca și regula de învățare a lui Hebb (1949), care a caracterizat învățarea ca fiind un rezultat al întăririi ponderilor în cazurile de activitate neurală.
Rizzuto și Kahana (2001) au reușit să demonstreze că modelul rețelei neurale poate explica repetarea acurateții rememorării prin încorporarea unui algoritm de învățare probabilistică. În timpul procesului de recuperare, nu are loc nicio învățare. Ca urmare, ponderile rețelei rămân fixe, arătând că modelul este capabil să treacă de la o etapă de învățare la una de reamintire. Adăugând deriva contextuală, ei au reușit să prezinte uitarea rapidă care are loc într-un model Hopfield în timpul unei sarcini de reamintire. Întreaga rețea contribuie la schimbarea activării oricărui singur nod.
Regula dinamică a lui McCulloch și Pitts (1943), care descrie comportamentul neuronilor, face acest lucru într-un mod care arată modul în care activările neuronilor multipli se mapează cu activarea ratei de declanșare a unui neuron nou și cum ponderile neuronilor întăresc conexiunile sinaptice dintre noul neuron activat și cei care l-au activat. Hopfield ar folosi regula dinamică a lui McCulloch-Pitts pentru a arăta cum este posibilă reamintirea în rețeaua Hopfield. Hopfield face însă acest lucru într-un mod repetitiv. Hopfield folosește o funcție de activare neliniară, în loc de una liniară. Prin urmare, aceasta creează regula dinamică Hopfield și cu aceasta, Hopfield a putut să arate că, cu funcția de activare neliniară, regula dinamică va modifica întotdeauna valorile vectorului de stare în direcția unuia dintre șabloanele stocate.
Note
[modificare | modificare sursă]- ^ F. Rosenblatt, "Perceptual Generalization over Transformation Groups", pp. 63--100 in Self-organizing Systems: Proceedings of an Inter-disciplinary Conference, 5 and 6 May, 1959. Edited by Marshall C. Yovitz and Scott Cameron. London, New York, [etc.], Pergamon Press, 1960. ix, 322 p.
- ^ Rosenblatt, Frank (). DTIC AD0256582: PRINCIPLES OF NEURODYNAMICS. PERCEPTRONS AND THE THEORY OF BRAIN MECHANISMS (în english). Defense Technical Information Center.
- ^ Eulogy: 1917 Karl Steinbuch 2005., by Bernard Widrow, Reiner Hartenstein, Robert Hecht-Nielsen, IEEE Computational Intelligence Society. page 5. August 2005.
- ^ Steinbuch, K. (). „Die Lernmatrix”. Kybernetik (în germană). 1 (1): 36–45. doi:10.1007/BF00293853. ISSN 1432-0770.
- ^ Steinbuch, Karl (). Automat und Mensch: über menschliche und maschinelle Intelligenz. Berlin: Springer. ISBN 978-3-642-53168-2.
- ^ Willshaw, D. J.; Buneman, O. P.; Longuet-Higgins, H. C. (iunie 1969). „Non-Holographic Associative Memory”. Nature. 222 (5197): 960–962. Bibcode:1969Natur.222..960W. doi:10.1038/222960a0. ISSN 0028-0836. PMID 5789326.
- ^ Kohonen, T. (aprilie 1974). „An Adaptive Associative Memory Principle”. IEEE Transactions on Computers. C–23 (4): 444–445. doi:10.1109/T-C.1974.223960. ISSN 0018-9340.
- ^ Glauber, Roy J. (februarie 1963). „Roy J. Glauber "Time-Dependent Statistics of the Ising Model"”. Journal of Mathematical Physics. 4 (2): 294–307. doi:10.1063/1.1703954. Accesat în .
- ^ Nakano, Kaoru (). „Learning Process in a Model of Associative Memory”. Pattern Recognition and Machine Learning. pp. 172–186. doi:10.1007/978-1-4615-7566-5_15. ISBN 978-1-4615-7568-9.
- ^ Nakano, Kaoru (). „Associatron-A Model of Associative Memory”. IEEE Transactions on Systems, Man, and Cybernetics. SMC-2 (3): 380–388. doi:10.1109/TSMC.1972.4309133.
- ^ Amari, Shun-Ichi (). „Learning patterns and pattern sequences by self-organizing nets of threshold elements”. IEEE Transactions. C (21): 1197–1206.
- ^ Little, W. A. (). „The Existence of Persistent States in the Brain”. Mathematical Biosciences. 19 (1–2): 101–120. doi:10.1016/0025-5564(74)90031-5.
- ^ Carpenter, Gail A (). „Neural network models for pattern recognition and associative memory”. Neural Networks. 2 (4): 243–257. doi:10.1016/0893-6080(89)90035-X. ISSN 0893-6080.
- ^ Sherrington, David; Kirkpatrick, Scott (). „Solvable Model of a Spin-Glass”. Physical Review Letters. 35 (26): 1792–1796. Bibcode:1975PhRvL..35.1792S. doi:10.1103/PhysRevLett.35.1792. ISSN 0031-9007.
- ^ a b c Hopfield, J. J. (). „Neural networks and physical systems with emergent collective computational abilities”. Proceedings of the National Academy of Sciences. 79 (8): 2554–2558. Bibcode:1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. PMC 346238
 . PMID 6953413.
. PMID 6953413.
- ^ a b Hopfield, J. J. (). „Neurons with graded response have collective computational properties like those of two-state neurons”. Proceedings of the National Academy of Sciences. 81 (10): 3088–3092. Bibcode:1984PNAS...81.3088H. doi:10.1073/pnas.81.10.3088. PMC 345226
 . PMID 6587342.
. PMID 6587342.
- ^ Engel, A.; Broeck, C. van den (). Statistical mechanics of learning. Cambridge, UK ; New York, NY: Cambridge University Press. ISBN 978-0-521-77307-2.
- ^ Seung, H. S.; Sompolinsky, H.; Tishby, N. (). „Statistical mechanics of learning from examples”. Physical Review A. 45 (8): 6056–6091. Bibcode:1992PhRvA..45.6056S. doi:10.1103/PhysRevA.45.6056.
- ^ a b Krotov, Dmitry; Hopfield, John (). „Dense Associative Memory for Pattern Recognition”. Neural Information Processing Systems. 29: 1172–1180.
- ^ Mete, Demircigil; et al. (). „On a model of associative memory with huge storage capacity”. Journal of Statistical Physics. 168 (2): 288–299. Bibcode:2017JSP...168..288D. doi:10.1007/s10955-017-1806-y.
- ^ Ramsauer, Hubert; et al. (). „Hopfield Networks is All You Need”. International Conference on Learning Representations.
- ^ Krotov, Dmitry; Hopfield, John (). „Large associative memory problem in neurobiology and machine learning”. International Conference on Learning Representations.
- ^ Hopfield, J. J. (). „Neural networks and physical systems with emergent collective computational abilities”. Proceedings of the National Academy of Sciences. 79 (8): 2554–2558. Bibcode:1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. PMC 346238
 . PMID 6953413.
. PMID 6953413.
- ^ MacKay, David J. C. (). „42. Hopfield Networks”. Information Theory, Inference and Learning Algorithms. Cambridge University Press. p. 508. ISBN 978-0521642989.
This convergence proof depends crucially on the fact that the Hopfield network's connections are symmetric. It also depends on the updates being made asynchronously.
- ^ a b c Bruck, J. (octombrie 1990). „On the convergence properties of the Hopfield model”. Proc. IEEE. 78 (10): 1579–85. doi:10.1109/5.58341.
- ^ a b c d Uykan, Z. (septembrie 2020). „On the Working Principle of the Hopfield Neural Networks and its Equivalence to the GADIA in Optimization”. IEEE Transactions on Neural Networks and Learning Systems. 31 (9): 3294–3304. doi:10.1109/TNNLS.2019.2940920. PMID 31603804.
- ^ Uykan, Z. (martie 2021). „Shadow-Cuts Minimization/Maximization and Complex Hopfield Neural Networks”. IEEE Transactions on Neural Networks and Learning Systems. 32 (3): 1096–1109. doi:10.1109/TNNLS.2020.2980237. PMID 32310787.
- ^ Hopfield, J.J.; Tank, D.W. (). „Neural computation of decisions in optimization problems”. Biological Cybernetics. 52 (3): 141–6. doi:10.1007/BF00339943. PMID 4027280.
- ^ Bruck, Jehoshua; Goodman, Joseph W (). „On the power of neural networks for solving hard problems”. Journal of Complexity. 6 (2): 129–135. doi:10.1016/0885-064X(90)90001-T. ISSN 0885-064X.
- ^ a b Storkey, A.J.; Valabregue, R. (). „The basins of attraction of a new Hopfield learning rule”. Neural Networks. 12 (6): 869–876. doi:10.1016/S0893-6080(99)00038-6. PMID 12662662.
- ^ Hebb 1949.
- ^ Storkey, Amos (). „Increasing the capacity of a Hopfield network without sacrificing functionality”. Artificial Neural Networks – ICANN'97. Lecture Notes in Computer Science. 1327. Springer. pp. 451–6. doi:10.1007/BFb0020196. ISBN 978-3-540-69620-9.
- ^ a b Hertz 1991.
- ^ Bruck, J.; Roychowdhury, V.P. (). „On the number of spurious memories in the Hopfield model (neural network)”. IEEE Transactions on Information Theory. 36 (2): 393–397. doi:10.1109/18.52486.
- ^ ABOUDIB, Ala; GRIPON, Vincent; JIANG, Xiaoran (). „A study of retrieval algorithms of sparse messages in networks of neural cliques”. COGNITIVE 2014 : The 6th International Conference on Advanced Cognitive Technologies and Applications. pp. 140–6. Bibcode:2013arXiv1308.4506A.
- ^ Amit, D.J. (). Modeling Brain Function: The World of Attractor Neural Networks. Cambridge University Press. ISBN 978-0-521-42124-9.
- ^ Rolls, Edmund T. (). Cerebral Cortex: Principles of Operation. Oxford University Press. ISBN 978-0-19-878485-2.










































