Secțiune

Pentru alte sensuri, vedeți Secțiune (dezambiguizare).

În geometrie și știință o secțiune este intersecția nevidă a unui corp tridimensional cu un plan, sau noțiunea analoagă din spații n-dimensionale. Tăierea unui obiect în felii creează mai multe secțiuni paralele. Frontiera unei secțiuni într-un spațiu tridimensional paralelă cu două dintre axe, adică paralelă cu planul determinat de aceste axe, este denumită uneori curbă de nivel. De exemplu, dacă un plan trece paralel cu solul prin munții dintr-o zonă, rezultatul este o curbă de nivel într-un spațiu bidimensional, care arată punctele de pe suprafața munților având aceeași cotă.

În desenul tehnic o secțiune este o proiecție plană, ortogonală, pe un plan paralel cu planul care intersectează corpul sau ansamblul de corpuri reprezentat. Ea este un instrument de bază pentru a descrie într-o imagine bidimensională structura internă a corpurilor tridimensionale. Tradițional, părțile solide sunt hașurate, modelele hașurilor indicând adesea tipurile de material folosite.

Prin tomografie computerizată^⁠(d), calculatoarele pot genera secțiuni transversale din datele obținute prin scanarea cu raze X.

Definiție

Dacă un plan intersectează un obiect solid tridimensional, atunci zona comună a planului cu solidul se numește secțiune a solidului.^[1]^[2] Planul care conține secțiunea prin solid se numește plan de secționare.^[3]

Forma secțiunii printr-un solid poate depinde de orientarea planului de secționare prin solid. De exemplu, în timp ce toate secțiunile unei bile sunt discuri,^[4] secțiunea printr-un cub depinde de orientarea planului de secționare. Dacă acest plan este perpendicular pe o dreaptă care unește centrele a două fețe, secțiunea va fi un pătrat, în timp ce dacă planul de secționare este perpendicular pe o diagonală a cubului care unește două vârfuri opuse, secțiunea poate fi un punct, un triunghi sau un hexagon.

Secțiuni plane

O noțiune înrudită este cea de secțiune plană, care este curba de intersecție a unui plan cu o suprafață.^[5] Astfel, o secțiune plană este frontiera unei secțiuni printr-un solid în planul de secționare.

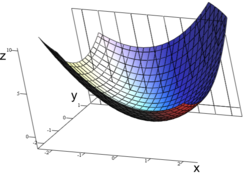
Dacă o suprafață într-un spațiu tridimensional este definită de o funcție de două variabile, adică $z=f(x,y)$ , secțiunile plane ale planelor de secționare care sunt paralele cu un plan de coordonate (un plan determinat de două axe de coordonate) se numesc curbe de nivel sau izolinii.^[6] Mai exact, planele de secționare ale căror ecuații sunt de forma $z=k$ (plane paralele cu planul $xy$ ) produc scțiuni plane denumite adesea în aplicații curbe de nivel.

Exemple matematice de secțiuni și secțiuni plane

O secțiune printr-un poliedru este un poligon.

Conicele — cercurile, elipsele, parabolele și hiperbolele — sunt secțiuni plane prin suprafața unui con, planele de secționare având diferite orientări, cum se vede în imaginea de alături.

Orice plan de secționare care trece prin centrul unui elipsoid produce o secțiune eliptică, în timp ce secțiunile plane corespunzătoare sunt elipse pe suprafața elipsoidului. Acestea degenerează în discuri, respectiv cercuri, atunci când planele de secționare sunt perpendiculare pe o anumită axă de simetrie. În general, secțiunile plane de forma cuadricelor sunt secțiuni conice.^[7]

O secțiune printr-un cilindru circular drept între două baze este un disc dacă secțiunea este paralelă cu baza cilindrului sau o zonă eliptică (v. figura de alături) dacă nu este nici paralel cu baza, nici perpendicular pe ea. Dacă planul de tăiere este perpendicular pe bază secțiunea este un dreptunghi (neprezentat). Dacă planul este doar tangent la cilindru secțiunea este doar un segment.

Prin „cilindru” se poate înțelege și doar suprafața laterală a unui cilindru solid. Dacă se folosește un „cilindru” în acest sens, paragraful de mai sus ar avea următorul cuprins: O secțiune plană a unui cilindru circular drept de lungime finită^[8] este un cerc dacă planul de secționare este perpendicular pe axa de simetrie a cilindrului sau o elipsă dacă nu este nici paralel, nici perpendicular pe acea axă. Dacă planul de secționare este paralel cu axa, secțiunea plană constă dintr-o pereche de segmente de dreaptă paralele, cu excepția cazului în care planul secant este tangent la cilindru, caz în care secțiunea plană este un singur segment.

Graficul funcției

z=x^{2}+xy+y^{2}

. Pentru derivata parțială în (1, 1, 3) și

y

constant, tangenta corespunzătoare este paralelă cu planul

xz

.

O secțiune plană prin graficul de mai sus prezentând curba de nivel din planul

xz

la

y=1

O secțiune plană poate fi utilizată pentru a vizualiza derivata parțială a unei funcții în raport cu unul dintre argumentele sale. Fie $z=f(x,y)$ . Cunoscând derivata parțială a lui $z=f(x,y)$ în funcție de $x$ , se poate obține o secțiune plană a funcției $f$ la o valoare fixă a lui $y$ pentru a trasa curba de nivel a $z$ numai în funcție de $x$ ; atunci derivata parțială în funcție de $x$ este panta graficului bidimensional rezultat.

Arii și volume

Principul Cavalieri spune că corpurile cu ale căror secțiuni corespondente au aceeași arie au același volum. Aria secțiunii ( $A'$ ) a unui obiect văzut dintr-un anumit unghi este aria totală a proiecției ortogonale a obiectului din acel unghi. De exemplu, un cilindru cu înălțimea $h$ și raza $r$ are $A'=\pi r^{2}$ când este văzut de-a lungul axei sale centrale și $A'=2rh$ atunci când este privit dintr-o direcție ortogonală. O sferă de rază $r$ are $A'=\pi r^{2}$ când este privită din orice unghi. Generic, $A'$ poate fi calculată prin evaluarea următoarei integrale de suprafață:

A'=\iint \limits _{\mathrm {sup} }d\mathbf {A} \cdot \mathbf {\hat {r}}

unde $\mathbf {\hat {r}}$ este versorul de-a lungul direcției de vizualizare către privitor, $d\mathbf {A}$ este un element de suprafață cu normala orientată spre exterior, iar integrala se face numai pe suprafața de deasupra, acea parte a suprafeței care este „vizibilă” din perspectiva privitorului. Pentru un corp convex, fiecare rază prin obiect din perspectiva privitorului intersectează doar două suprafețe. Pentru astfel de obiecte integrala poate fi efectuată pe întreaga suprafață ( $A$ ) luând valoarea absolută a integrandului (astfel încât să nu se facă diferența între „partea de sus” și „partea de jos” a obiectului, așa cum ar fi cerut de teorema divergenței aplicată câmpului vector constant $\mathbf {\hat {r}}$ ) și împărțind la doi:

A'={\frac {1}{2}}\iint \limits _{A}|d\mathbf {A} \cdot \mathbf {\hat {r}} |

În dimensiuni superioare

În analogie cu secțiunea printr-un solid, secțiunea unui corp $n$ -dimensional dintr-un spațiu $n$ -dimensional este intersecția nevidă a corpului cu un hiperplan (un subspațiu $n$ –1)-dimensional). Acest concept a fost uneori folosit pentru a ajuta la vizualizarea aspectelor spațiilor cu dimensiuni superioare.^[9] De exemplu, dacă un obiect cvadridimensional trece prin spațiul nostru tridimensional, am vedea o secțiune tridimensională a obiectului cvadridimensional. În special, o 4-bilă care trece prin 3-spațiu ar apărea ca o 3-bilă care în timpul tranziției crește la maxim și apoi scade. Acest obiect dinamic (din punctul de vedere al spațiului tridimensional) este o succesiune de secțiuni ale 4-bilei.

Exemple din știință


În geologie, structura interiorului unei planete este adesea ilustrată folosind o secțiune care trece prin centrul ei. În imagine este o secțiune prin interiorul Pământului.	Secțiunile sunt adesea folosite în anatomie pentru a ilustra structura interioară a unui organ. În imagine este o secțiune a mezencefalului la nivelul coliculului superior.	Secțiune transversală printr-un trunchi de Pinus taeda, care arată inelele anuale de creștere, care pot fi utilizate pentru a afla vârsta arborelui și variațiile în timp ale mediului său.

Note

^ Săucan ș.a., Desen…, p. 76
^ Swokowski 1983, p. 296.
^ Săucan ș.a., Desen…, p. 78
^ În limbajul matematic secțiunile unei 2-sfere (sferă) sunt 1-sfere (cercuri).
^ Albert 2016, p. 38.
^ Swokowski 1983, p. 716.
^ Albert 2016, p. 117.
^ Acești cilindri sunt deschiși, nu conțin bazele lor.
^ Stewart 2001, p. 59.

Bibliografie

Săucan (coord.), Alexandru; Moncea, Jean; Tacorian, Teodor; Tomuță, Alexandru (1970). Geometrie descriptivă și desen tehnic: Partea a II-a — desen industrial. București: Ed. Didactică și Pedagogică.
en Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
en Stewart, Ian (2001), Flatterland / like flatland, only more so, Persus Publishing, ISBN 0-7382-0675-X
en Swokowski, Earl W. (1983), Calculus with analytic geometry (ed. Alternate), Prindle, Weber & Schmidt, ISBN 0-87150-341-7

Vezi și

Legături externe

Materiale media legate de secțiune la Wikimedia Commons

[1] Săucan ș.a., Desen…, p. 76

[2] Swokowski 1983, p. 296.

[3] Săucan ș.a., Desen…, p. 78

[4] În limbajul matematic secțiunile unei 2-sfere (sferă) sunt 1-sfere (cercuri).

[5] Albert 2016, p. 38.

[6] Swokowski 1983, p. 716.

[7] Albert 2016, p. 117.

[8] Acești cilindri sunt deschiși, nu conțin bazele lor.

[9] Stewart 2001, p. 59.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]