Triangulare în evantai
Aspect
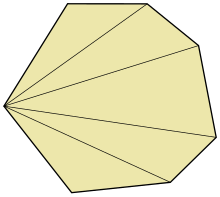

În geometria algoritmică(d) o triangulare în evantai este o modalitate simplă de a triangula un poligon alegând un vârf și desenând laturile spre toate celelalte vârfuri ale poligonului. Nu orice poligon poate fi triangulat în acest fel, așa că această metodă este de obicei folosită în special pentru poligoane convexe.[1]
Proprietăți
[modificare | modificare sursă]Pe lângă proprietățile tuturor triangulărilor, triangulările în evantai au următoarele proprietăți:
- Toate poligoanele convexe, dar nu toate poligoanele, pot fi triangulate în evantai.
- Poligoanele cu un singur vârf concav pot fi întotdeauna triangulate în evantai dacă diagonalele sunt trasate pornind din vârful concav.
- Se poate ști dacă un poligon poate fi triangulat în evantai prin rezolvarea problemei galeriei de artă, pentru a determina dacă există cel puțin un vârf care este vizibil din fiecare punct al poligonului.
- Triangularea unui poligon cu n vârfuri necesită n−3 diagonale și generează n−2 triunghiuri.[2]
- Generarea listei de triunghiuri este trivială dacă este disponibilă o listă ordonată de vârfuri și poate fi calculată în timp liniar. Ca atare, nu este necesară stocarea explicită a listei de triunghiuri. Multe biblioteci grafice implementează primitive pentru a reprezenta poligoane bazate pe această triangulare.[3]
- Deși această triangulare este potrivită pentru rezolvarea anumitor probleme, cum ar fi rasterizarea sau detectarea coliziunilor(d), poate fi inadecvată pentru alte sarcini, deoarece vârful de origine acumulează un număr mare de vecini, iar unghiurile interioare ale triangulării sunt distribuite neuniform.
Note
[modificare | modificare sursă]- ^ en Loera, Jesus; Rambau, Joerg; Santos, Francisco (). Triangulations: Structures for Algorithms and Applications
 . Springer Science & Business Media. pp. 103. ISBN 9783642129711.
. Springer Science & Business Media. pp. 103. ISBN 9783642129711.
- ^ en O'Rourke, Joseph (). Computational geometry in C (ed. 2nd). Cambridge, UK: Cambridge University Press. ISBN 9780521649766. OCLC 38542796.
- ^ en Segal, Mark (). „The OpenGL Graphics System: A Specification” (PDF). Accesat în .
