Endecaedru

(animație)
În geometrie un endecaedru este un poliedru cu 11 fețe. Există numeroase forme topologic distincte ale unui endecaedru, de exemplu piramida decagonală și prisma eneagonală.
Trei forme sunt poliedre Johnson: piramida pentagonală alungită J9, prisma triunghiulară biaugmentată J50 și prisma hexagonală augmentată J54.
Două clase, endecaedrele bisimetrice și sfenoide sunt poliedre care umplu spațiul.[1]
Endecaedrul comun
[modificare | modificare sursă]Dintre toate endecaedrele convexe, excluzând imaginile în oglindă, există un total de 440 564 de endecaedre convexe topologic distincte, având cel puțin 8 vârfuri.[2] Adică între aceste cazuri există diferențe semnificative în structura topologică, ceea ce înseamnă că două tipuri de poliedre nu pot fi transformate prin deplasarea pozițiilor vârfurilor, rotirea sau scalarea. Nu se pot interschimba, așa că structura lor topologică este diferită.
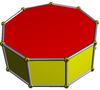
Endecaedre comune sunt formele conice, cilindrice, unele poliedre Johnson, și un poliedru semiregulat, care nu este unul arhimedic, ci prisma eneagonală.
|

|

|

|

|

|
| Prismă eneagonală | Piramidă decagonală | Piramidă pentagonală alungită | Dualul piramidei pentagonale alungite | Prismă triunghiulară rectificată | Endecaedru bisimetric |
Endecaedrul bisimetric
[modificare | modificare sursă]
Endecaedrul bisimetric este un poliedru care umple spațiul, care poate fi asamblat în straturi de tetrameri „în formă de barcă” care se întrepătrund, care la rândul lor sunt apoi stivuiți pentru a umple spațiul. Prin urmare, este un analog tridimensional al pavării pentagonale Cairo.
Endecaedrul sfenoid
[modificare | modificare sursă]Endecaedrul sfenoid este un poliedru care umple spațiul, care poate fi asamblat în straturi ale pavării pentagonale floare, care la rândul lor sunt stivuite pentru a umple spațiul.
Note
[modificare | modificare sursă]Bibliografie
[modificare | modificare sursă]- en Thomas H. Sidebotham. The A to Z of Mathematics: A Basic Guide. John Wiley & Sons. 2003: 237. ISBN: 9780471461630
- en Inchbald, Guy (). „Five space-filling polyhedra”. The Mathematical Gazette. 80 (489): 466–475. doi:10.2307/3618509. ISSN 0025-5572. JSTOR 3618509. Zbl 0885.52011. [1]
- en Space-Filling Bisymmetric Hendecahedron. [2013-04-11]
- en Anderson, Ian. "Constructing Tournament Designs." The Mathematical Gazette 73, no. 466 (December 1989): 284-292
- en Holleman, A. F.; Wiberg, E., Inorganic Chemistry, San Diego: Academic Press: 1165, 2001, ISBN: 0-12-352651-5
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Undecahedron la MathWorld.
| |||||||||||||||||||||||||||



