Hexadecaedru
În geometrie un hexadecaedru este un poliedru cu 16 fețe. Există numeroase forme topologic distincte de hexadecaedre, de exemplu piramida pentadecagonală, bipiramida octogonală, prisma tetradecagonală și antiprisma heptagonală.
Nu există niciun hexadecaedru regulat. Patru sunt poliedre Johnson: piramida pentagonală giroalungită (J11), bipiramida pătrată giroalungită (J17), dodecaedrul augmentat (J58) și cubul trunchiat biaugmentat (J67).
Forme convexe
[modificare | modificare sursă]Există 387 591 510 244 de hexadecaedre convexe topologic distincte, excluzând imaginile în oglindă, având cel puțin 10 vârfuri.[1] Adică între aceste cazuri există diferențe semnificative în structura topologică, ceea ce înseamnă că două tipuri de poliedre nu pot fi transformate prin deplasarea pozițiilor vârfurilor, rotirea sau scalarea. Nu se pot interschimba, așa că structura lor topologică este diferită.
Hexadecaedre autoduale
[modificare | modificare sursă]Există 302 404 hexadecaedre autoduale, 1476 cu ordinul de simetrie de cel puțin 2.[2] Autodualul cu simetrie înaltă are simetrie tetraedrică chirală și poate fi realizat topologic prin eliminarea a 4 din 20 de vârfuri ale unui dodecaedru regulat și se numește dodecaedru diminuat tetraedric.
Exemple de hexadecaedre convexe
[modificare | modificare sursă]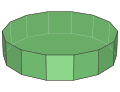
|

|
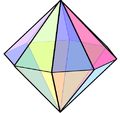
|

|

|

|
| Prismă tetradecagonală | Antiprismă heptagonală | Bipiramidă octogonală | Piramidă pentagonală giroalungită (J11) | Bipiramidă pătrată giroalungită (J17) | Dodecaedru augmentat (J58) |
Hexadecaedre neconvexe
[modificare | modificare sursă]
Un hexadecaedru neconvex interesant este hexadecaedrul toroidal din figura alăturată. În spațiul cvadridimensional, cu simbolul Schläfli {4,4|4}, are toate fețele pătrate și este un subset al tesseractului.
Note
[modificare | modificare sursă]Legături externe
[modificare | modificare sursă]- en What Are Polyhedra?, cu prefixe numerice grecești



