Forma universului

Forma universului este geometria locală și globală a universului. Caracteristicile locale ale geometriei universului sunt descrise în primul rând prin curbura sa, în timp ce topologia universului descrie proprietățile globale generale ale formei sale ca pe un obiect continuu. Forma universului este legată de relativitatea generală, care descrie spațiu-timp ca fiind curbat și îndoit de masă și energie.

Forma exactă a Universului este încă o chestiune aflată în dezbatere în cosmologia fizică, dar datele experimentale din diverse surse independente (WMAP, BOOMERanG și Planck, de exemplu) confirmă faptul că universul observabil este plat, cu o marjă de eroare de 0,4%.^[1]^[2]^[3] Teoreticienii au încercat să construiască un model matematic formal al formei universului. Modelul pe care majoritatea teoreticienilor îl folosesc în prezent este modelul Friedmann-Lemaître-Robertson-Walker (FLRW).

Au fost prezentate argumentele conform cărora datele observaționale se potrivesc cel mai bine cu concluzia că forma universului global este infinită și plată,^[4] dar datele sunt, de asemenea, în concordanță cu alte forme posibile, cum ar fi așa-numitul spațiul dodecaedric Poincaré^[5]^[6]^[7] și spațiul Sokolov-Starobinskii.^[8]

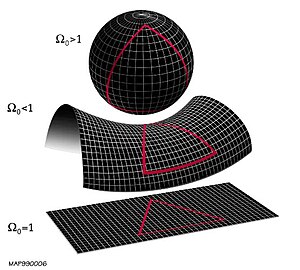
Un parametru important care determină teoria evoluției viitoare a Universului este parametrul de densitate, Omega (Ω), definit ca densitatea medie a materiei a universului împărțită la o valoare critică a acelei densități.

Dacă $Ω = 1$ , universul este plat; expansiunea va continua la nesfârșit, dar componentele universului vor fi separate de distanțe infinite doar după pierderea unor cantități de energie cinetică.
Dacă $Ω > 1$ , există o curbură pozitivă; interacțiunile gravitaționale devin predominante și expansiunea se poate opri sau chiar inversa, ducând la colapsul întregului univers.
Dacă $Ω < 1$ există o curbură negativă; expansiunea va continua până când componentele universului sunt separate de distanțe infinite.

Vezi și

Uroš Seljak

Note

^ „Will the Universe expand forever?”. NASA. 24 ianuarie 2014. Accesat în 16 martie 2015.
^ „Our universe is Flat”. FermiLab/SLAC. 7 aprilie 2015.
^ Marcus Y. Yoo (2011). „Unexpected connections”. Engineering & Science. LXXIV1: 30.
^ Demianski, Marek; Sánchez, Norma; Parijskij, Yuri N. (2003). Topology of the universe and the cosmic microwave background radiation. The Early Universe and the Cosmic Microwave Background: Theory and Observations. Proceedings of the NATO Advanced Study Institute. The early universe and the cosmic microwave background: theory and observations. 130. Springer. p. 161. Bibcode:2003eucm.book..159D. ISBN 978-1-4020-1800-8.
^ Luminet, Jean-Pierre; Weeks, Jeff; Riazuelo, Alain; Lehoucq, Roland; Uzan, Jean-Phillipe (9 octombrie 2003). „Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background”. Nature. 425 (6958): 593–5. arXiv:astro-ph/0310253 . Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579.
^ "Is the universe a dodecahedron?", article at PhysicsWeb.
^ Roukema, Boudewijn; Zbigniew Buliński; Agnieszka Szaniewska; Nicolas E. Gaudin (2008). „A test of the Poincare dodecahedral space topology hypothesis with the WMAP CMB data”. Astronomy and Astrophysics. 482 (3): 747. arXiv:0801.0006 . Bibcode:2008A&A...482..747L. doi:10.1051/0004-6361:20078777.
^ Aurich, Ralf; Lustig, S.; Steiner, F.; Then, H. (2004). „Hyperbolic Universes with a Horned Topology and the CMB Anisotropy”. Classical and Quantum Gravity. 21 (21): 4901–4926. arXiv:astro-ph/0403597 . Bibcode:2004CQGra..21.4901A. doi:10.1088/0264-9381/21/21/010.

Legături externe

How do we know that the universe is flat A video explains how astrophysicists measure the geometry of the universe at Physicsworld.com

[NASA_Shape-1] „Will the Universe expand forever?”. NASA. 24 ianuarie 2014. Accesat în 16 martie 2015.

[Fermi_Flat-2] „Our universe is Flat”. FermiLab/SLAC. 7 aprilie 2015.

[3] Marcus Y. Yoo (2011). „Unexpected connections”. Engineering & Science. LXXIV1: 30.

[4] Demianski, Marek; Sánchez, Norma; Parijskij, Yuri N. (2003). Topology of the universe and the cosmic microwave background radiation. The Early Universe and the Cosmic Microwave Background: Theory and Observations. Proceedings of the NATO Advanced Study Institute. The early universe and the cosmic microwave background: theory and observations. 130. Springer. p. 161. Bibcode:2003eucm.book..159D. ISBN 978-1-4020-1800-8.

[Nat03-5] Luminet, Jean-Pierre; Weeks, Jeff; Riazuelo, Alain; Lehoucq, Roland; Uzan, Jean-Phillipe (9 octombrie 2003). „Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background”. Nature. 425 (6958): 593–5. arXiv:astro-ph/0310253 . Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579.

[physwebLum03-6] "Is the universe a dodecahedron?", article at PhysicsWeb.

[RBSG08-7] Roukema, Boudewijn; Zbigniew Buliński; Agnieszka Szaniewska; Nicolas E. Gaudin (2008). „A test of the Poincare dodecahedral space topology hypothesis with the WMAP CMB data”. Astronomy and Astrophysics. 482 (3): 747. arXiv:0801.0006 . Bibcode:2008A&A...482..747L. doi:10.1051/0004-6361:20078777.

[Aurich0403597-8] Aurich, Ralf; Lustig, S.; Steiner, F.; Then, H. (2004). „Hyperbolic Universes with a Horned Topology and the CMB Anisotropy”. Classical and Quantum Gravity. 21 (21): 4901–4926. arXiv:astro-ph/0403597 . Bibcode:2004CQGra..21.4901A. doi:10.1088/0264-9381/21/21/010.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]