Rep-dală

În pavările geometrice o rep-dală[a] este o formă care poate fi divizată în copii mai mici de aceeași formă. În 2012, Lee Sallows a publicat în Mathematics Magazine o generalizare a rep-dalelor numită „seturi de dale care se autopavează”.[2]

Terminologie
[modificare | modificare sursă]
O rep-dală este etichetată rep-n dacă divizarea utilizează n copii. O astfel de formă formează în mod necesar dala pentru o pavare a planului, în multe cazuri o pavare aperiodică(d). O divizare a rep-dalei folosind diferite dimensiuni ale formei inițiale se numește rep-dală neregulată sau irrep-dală. Dacă divizarea folosește n copii, se spune că forma este irrep-n. Dacă toate aceste subdale sunt de dimensiuni diferite, atunci pavarea este descrisă în plus ca fiind perfectă. O formă care este rep-n sau irrep-n este trivial și irrep-(kn − k + n) pentru orice k > 1, prin înlocuirea celei mai mici dale din divizare rep-n cu n dale mai mici. Ordinul unei forme, indiferent dacă se utilizează rep-dale sau irrep-dale, este cel mai mic număr posibil de dale care ar fi suficient.[3]
Exemple
[modificare | modificare sursă]
Orice pătrat, dreptunghi, paralelogram, romb sau triunghi este rep-4. Poliamantul Sfinx (ilustrat mai sus) este rep-4 și rep-9 și este unul dintre puținele pentagoane care se poate autoreplica. Insula Gosper este rep-7. Fulgul lui Koch(d) este irrep-7: șase fulgi mici de aceeași dimensiune, împreună cu un alt fulg cu suprafața de trei ori mai mare decât cei mici, se pot combina pentru a forma un singur fulg mai mare.
Un triunghi dreptunghic cu raportul catetelor de 1:2 este rep-5, iar divizarea sa rep-5 formează baza unei pavări aperiodice. Conform teoremei lui Pitagora, ipotenuza are o lungime de √5.
Standardul internațional ISO 216 definește dimensiunile foilor de hârtie folosind raportul laturilor de √2. Dreptunghiurile în această formă sunt rep-2. Un dreptunghi (sau paralelogram) este rep-n dacă raportul său de aspect este √n:1. Un triunghi dreptunghic isoscel este, de asemenea, rep-2.
Rep-dale și simetrie
[modificare | modificare sursă]Unele rep-dale, ca pătratul și triunghiul echilateral, sunt simetrice și rămân identice atunci când se reflectă într-o oglindă. Altele, precum sfinxul, sunt asimetrice și există în două forme distincte legate prin reflexia în oglindă. Divizarea sfinxului și a altor rep-dale asimetrice necesită utilizarea atât a formei originale, cât și a imaginii în oglindă.
Rep-dale și poliforme
[modificare | modificare sursă]Unele rep-dale se bazează pe poliforme, cum ar fi poliamantele și poliominourile, sau forme create prin așezarea triunghiurilor echilaterale și a pătratelor latură la latură.
Pătrate
[modificare | modificare sursă]
Daca un poliomino este rectificabil, adica capabil sa paveze un dreptunghi, atunci va fi și rep-dală, deoarece dreptunghiul va avea un raport intreg între lungimile laturilor și astfel se va pava ca pătratul. Acest lucru poate fi văzut la octominouri, care sunt create din opt pătrate. Două copii ale unor octominouri vor pava un pătrat; prin urmare aceste octominouri sunt și dale rep-16.
Patru copii ale unor nonominouri și pseudo poliomonouri vor pava un pătrat, prin urmare aceste poliforme sunt și dale rep-36.

Triunghiuri echilaterale
[modificare | modificare sursă]Similar, dacă un poliamant pavează un triunghi echilateral, va fi și o rep-dală.

 |
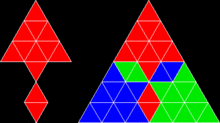 |
Triunghiuri dreptunghice
[modificare | modificare sursă]Un triunghi dreptunghic este un triunghi care are un unghi drept (de 90°). Două forme particulare de triunghi dreptunghic au atras atenția cercetătorilor rep-dalelor, triunghiul 45°-90°-45° și triunghiul 30°-60°-90°.
Triunghiuri 45°-90°-45°
[modificare | modificare sursă]Poliformele formate din triunghiuri dreptunghice isoscele, cu laturile în raportul 1 : 1 : √2, sunt cunoscute ca poliabolouri. Un număr infinit dintre ele sunt rep-dale. Într-adevăr, cel mai simplu dintre toate rep-dalele este triunghiul dreptunghic isoscel. Este rep-2 când este divizat cu o singură dreaptă care bisectează unghiul drept. Rep-2 rep-dalele sunt, de asemenea, rep-2n, iar triunghiurile rep-4,8,16+ produc rep-dale în continuare. Acestea sunt generate eliminând jumătate din subcopii și permutând restul până când sunt simetrice în oglindă într-un triunghi dreptunghic. Cu alte cuvinte, două copii vor pava un triunghi dreptunghic. Unul dintre aceste noi rep-dale amintește de peștele format din trei triunghiuri echilaterale.

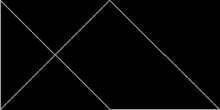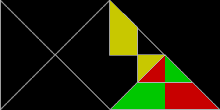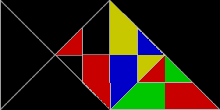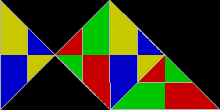
Triunghiuri 30°-60°-90°
[modificare | modificare sursă]Poliformele formate din triunghiuri dreptunghice 30°-60°-90°, cu laturile în raportul 1 : √3 : 2, sunt cunoscute ca polidraftere. Unele sunt identice cu poliamantele.[4]
Rep-dale multiple și variante
[modificare | modificare sursă]Multe dintre rep-dalele obișnuite sunt rep-n2 pentru toate valorile întregi pozitive ale n. Acest lucru este valabil în special pentru trei trapeze, inclusiv cel format din trei triunghiuri echilaterale, pentru trei hexagoane paralele cu axele (L-triomino, L-tetromino și P-pentomino) și sfinxul hexiamant.[5] În plus, multe rep-dale, în special cele cu rep-n mai mare, pot fi autopavate în diferite moduri. De exemplu, rep-9 L-tetramino are cel puțin paisprezece astfel de pavări diferite. Sfinxul rep-9 hexiamant poate fi, de asemenea, pavat în diferite moduri.
 |
 |
Rep-dale cu infinite laturi
[modificare | modificare sursă]

Cele mai cunoscute rep-dale sunt poligoane cu un număr finit de laturi, dar unele forme cu un număr infinit de laturi pot fi și ele rep-dale. De exemplu, triunghiul teragonic (triunghiul cu coarne), este rep-4. Este, de asemenea, un exemplu de fractal rep-dală.
Rep-dale pentagonale
[modificare | modificare sursă]Rep-dalele triunghiulare și patrulatere sunt comune, dar rep-dalele pentagonale sunt rare. Pentru o lungă perioadă de timp, sfinxul a fost considerat a fi singurul exemplu cunoscut, dar matematicianul germano-neo zeelandez Karl Scherer și cel american George Sicherman au găsit mai multe exemple, inclusiv o piramidă dublă și o versiune alungită a sfinxului. Totuși, sfinxul și versiunile sale extinse sunt singurele pentagoane cunoscute care pot fi pavate cu copii de forma lor, egale.[6]<ref>
Note explicative
[modificare | modificare sursă]- ^ Joc de cuvinte intraductibil. În engleză rep-tile, provine de la replicate (a se replica) și tile (dală) și a fost inventat ca un calambur de la reptile de către matematicianul recreativ Solomon W. Golomb și popularizat de Martin Gardner în rubrica sa Mathematical Games din numărul din mai 1963 al revistei Scientific American.[1]
Note
[modificare | modificare sursă]- ^ en A Gardner's Dozen—Martin's Scientific American Cover Stories
- ^ Sallows (2012).
- ^ Gardner (2001).
- ^ en Polydrafter Irreptiling
- ^ Nițică (2003).
- ^ en Klarke, Andrew, Reptiles, recmath.com, accesat 2024-04-26
Bibliografie
[modificare | modificare sursă]- en Gardner, M. (), „Rep-tiles”, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, New York: W. W. Norton, pp. 46–58
- en Gardner, M. (), „Chapter 19: Rep-tiles, Replicating Figures on the Plane”, The Unexpected Hanging and Other Mathematical Diversions, Chicago, IL: Chicago University Press, pp. 222–233
- en Langford, C. D. (), „Uses of a Geometric Puzzle”, The Mathematical Gazette, 24 (260): 209–211, doi:10.2307/3605717
- en Nițică, Viorel (), „Rep-tiles revisited”, MASS selecta, Providence, RI: American Mathematical Society, pp. 205–217, MR 2027179
- en Sallows, Lee (), „On self-tiling tile sets”, Mathematics Magazine, 85 (5): 323–333, doi:10.4169/math.mag.85.5.323, MR 3007213
- en Scherer, Karl (), A Puzzling Journey to the Reptiles and Related Animals
- en Wells, D. (), The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, pp. 213–214
Legături externe
[modificare | modificare sursă]![]() Materiale media legate de rep-dală la Wikimedia Commons
Materiale media legate de rep-dală la Wikimedia Commons
- Rep-dale
- en Mathematics Centre Sphinx Album
- en Eric W. Weisstein, Rep-Tile la MathWorld.
- en IFStile - program for finding rep-tiles
- Irrep-dale








