Rotondă (geometrie)
Aspect
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
Acest articol se referă la o figură geometrică. Pentru alte sensuri, vedeți rotondă.
| Rotondă | |
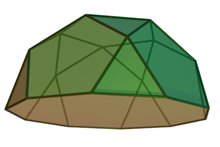 | |
| Exemplu: rotondă pentagonală | |
| Descriere | |
|---|---|
| Fețe | 2n triunghiuri, n pentagoane 1 n-gon 1 2n-gon |
| Laturi (muchii) | 7n |
| Vârfuri | 4n |
| χ | 2 |
| Grup de simetrie | Cnv, [n], (*nn), ordin 2n |
| Grup de rotație | Cn, [n]+, (nn), ordin n |
| Proprietăți | convexă |
În geometrie o rotondă este un poliedru format din două poligoane, unul (baza) cu de două ori mai multe laturi decât celălalt, unite printr-o bandă alternantă de triunghiuri isoscele și pentagoane. Dacă triunghiurile sunt echilaterale și pentagoanele, baza și fața ei opusă sunt regulate, există un singur astfel de poliedru, rotonda pentagonală, care este poliedrul Johnson J6.

Există un număr infinit de rotonde la care fețele nu sunt regulate. Toate au simetrie ciclică.
Bibliografie
[modificare | modificare sursă]- en Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- en Zalgaller, Victor (). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.

