Bipiramidă decagonală
| Bipiramidă decagonală | |
 | |
| Descriere | |
|---|---|
| Tip | bipiramidă |
| Fețe | 20 triunghiuri isoscele |
| Laturi (muchii) | 30 |
| Vârfuri | 12 |
| χ | 2 |
| Configurația feței | V4.4.10 |
| Simbol Schläfli | { } + {10} |
| Diagramă Coxeter | |
| Grup de simetrie | D10h, [10,2], (*2.2.10), ordin 40 |
| Grup de rotație | D10, [10,2]+, (2.2.10), ordin 20 |
| Poliedru dual | prismă decagonală |
| Proprietăți | convexă, tranzitivă pe fețe[1] |

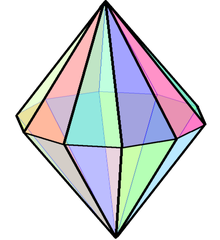
În geometrie o bipiramidă decagonală este un poliedru format prin unirea a două piramide decagonale prin bazele lor. O bipiramidă decagonală are 20 de fețe triunghiulare, 30 de laturi (muchii) și 12 vârfuri.
Deși este tranzitivă pe fețe,[1] nu este un poliedru platonic deoarece în unele vârfuri se întâlnesc câte patru fețe, iar în altele câte zece. Nu este nici poliedru Johnson deoarece fețele sale nu pot fi triunghiuri echilaterale; într-un spațiu tridimensional 10 triunghiuri echilaterale pot avea un vârf comun doar într-un spațiu hiperbolic.
Este una dintr-o mulțime infinită de bipiramide. Având 20 de fețe, este un tip de icosaedru deși acest nume este de obicei asociat cu forma poliedrului regulat cu fețe triunghiulare. De aceea denumirea de „icosaedru” este rareori folosită fără precizări suplimentare.
Bipiramida decagonală are un plan de simetrie (orizontal în figura din dreapta) unde bazele celor două piramide sunt unite. Secțiunea în acest plan este un decagon. De asemenea, există zece plane de simetrie care trec prin cele două apexuri, situate la unghiuri de 18° unul față de celălalt și sunt perpendiculare pe planul orizontal. Secțiunile din aceste plane sunt romburi.
Formule pentru bipiramida regulată dreaptă
[modificare | modificare sursă]Pentru o bipiramidă decagonală regulată cu latura a și semiînălțimea h (jumătate din distanța dintre apexuri) aria A este dată de formula:[2][3]
Pentru a = 1 și h = 1 aria este ≈ 18,3522042.
Formula volumului V este:[2][3]
Pentru a = 1 și h = 1 volumul este ≈ 5,1294726.
Pavare sferică
[modificare | modificare sursă]
Poate fi văzută ca o pavare a unei sfere, fețele reprezentând și domeniile fundamentale ale simetriei diedrale [5,2], *522.
Poliedre înrudite
[modificare | modificare sursă]| Numele bipiramidei |
Bipiramidă digonală |
Bipiramidă triunghiulară (v. J12) |
Bipiramidă tetragonală (v. O) |
Bipiramidă pentagonală (v. J13) |
Bipiramidă hexagonală |
Bipiramidă heptagonală |
Bipiramidă octogonală |
Bipiramidă eneagonală |
Bipiramidă decagonală |
... | Bipiramidă apeirogonală |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Imagine | 
|

|

|

|

|

|
... | ||||
| Pavare sferică | 
|

|

|

|

|

|

|

|

|
Pavare plană | |
| Config. feței | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ... | V∞.4.4 |
| Diagramă Coxeter | ... |
| Variante de pavări omnitrunchiate cu simetrie *n42: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetrie *n42 [n,3] |
Sferice | Euclidiană | Hiperbolice compacte | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Figuri omnitrunchiate |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Duale omnitrunchiate |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
Note
[modificare | modificare sursă]- ^ a b en „duality”. maths.ac-noumea.nc. Accesat în .
- ^ a b en Right Regular Pyramid Calculator, rechneronline.de, accesat 2022-10-29
- ^ a b en Eric W. Weisstein, Trigonometry Angles--Pi/10 la MathWorld.
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Dipyramid la MathWorld.
- en Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- <10> Arhivat în , la Wayback Machine. model VRML
- Conway Notation for Polyhedra Cheie: dP10


