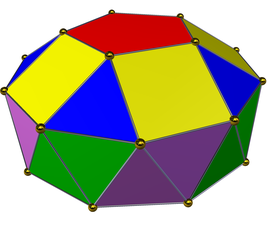
Bicupolă pentagonală giroalungită
| Bicupolă pentagonală giroalungită | |
 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J45 – J46 – J47 |
| Fețe | 42 (30 triunghiuri echilaterale 10 pătrate) 2 pentagoane)[1] |
| Laturi (muchii) | 70[1] |
| Vârfuri | 30[1] |
| χ | 2 |
| Configurația vârfului | 10 (3.4.5.4); 20 (34.4) |
| Grup de simetrie | D5, [5,2]+, (225), ordin 10 |
| Arie | ≈ 26,431 a2 (a = latura) |
| Volum | ≈ 11,397 a3 (a = latura) |
| Poliedru dual | – |
| Proprietăți | convexă, chirală |
| Desfășurată | |
 | |
În geometrie bicupola pentagonală giroalungită este un poliedru convex construit prin giroalungirea unei bicupole pentagonale (fie o ortobicupolă pentagonală, J30, fie o girobicupolă pentagonală, J31) prin inserarea unei antiprisme decagonale între cele două jumătăți. Este poliedrul Johnson J46.[1][2]
Bicupola pentagonală giroalungită este unul dintre cele cinci poliedre Johnson care sunt chirale, ceea ce înseamnă că au o formă „pe stânga” și una „pe dreapta”. În imaginile de mai jos, fiecare față pătrată din imaginea din stânga este conectată printr-o cale de două fețe triunghiulare (colorate violet) de o față pătrată de sus și la stânga. În figura cu chiralitate opusă (imaginea de mai jos din dreapta), fiecare față pătrată de jos este conectată la o față pătrată de sus și la dreapta. Cele două forme chirale ale lui J46 nu sunt considerate poliedre Johnson diferite.
-
varianta „pe stânga”
-
varianta „pe dreapta”
Mărimi asociate
[modificare | modificare sursă]Următoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:
Aria este suma ariei ortobicupolei pentagonale plus aria celor 20 triunghiuri ale antiprismei decagonale:
Volumul este suma volumelor ortobicupolei pentagonale plus a antiprismei decagonale:
Note
[modificare | modificare sursă]- ^ a b c d en Stephen Wolfram, "Gyroelongated pentagonal bicupola" from Wolfram Alpha. Retrieved December 17, 2022.
- ^ en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603