Rombicosidodecaedru metabigirat
| Rombicosidodecaedru metabigirat | |
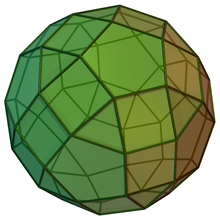 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J73 – J74 – J75 |
| Fețe | 62 (20 triunghiuri echilaterale 30 pătrate 12 pentagoane)[1] |
| Laturi (muchii) | 120[1] |
| Vârfuri | 60[1] |
| χ | 2 |
| Configurația vârfului | 20 (3.42.5); 40 (3.4.5.4) |
| Grup de simetrie | C2v , [2], (*22), ordin 4 |
| Arie | ≈ 59,306 a2 (a = latura) |
| Volum | ≈ 41,615 a3 (a = latura) |
| Poliedru dual | – |
| Proprietăți | convex, canonic |
| Desfășurată | |
 | |
În geometrie un rombicosidodecaedru metabigirat este un poliedru convex, poliedrul Johnson J74.[1][2]
Este un poliedru canonic. Având 62 de fețe, este un hexacontadiedru.
Construcție
[modificare | modificare sursă]Poate fi construit prin rotirea cu 36° a două cupole pentagonale (J5) care nu sunt opuse ale unui rombicosidodecaedru (un poliedru arhimedic). Rombicosidodecaedrul metabigirat are aceleași fețe în jurul unui vârf, ca și rombicosidodecaedrul, dar are la unele vârfuri configurația vârfului diferită: 3.4.4.5, față de cea a rombicosidodecaedrului, 3.4.5.4.
Mărimi asociate
[modificare | modificare sursă]Următoarele formule pentru arie, A, volum, V, rază mediană, rm și rază circumscrisă, R, sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Poliedre înrudite
[modificare | modificare sursă]Alte poliedre Johnson alternative, construite prin rotirea diferitelor cupole ale unui rombicosidodecaedru, sunt:
- rombicosidodecaedrul girat (J72) la care este rotită o singură cupolă;
- rombicosidodecaedrul parabigirat (J73) la care sunt rotite două cupole opuse;
- rombicosidodecaedrul trigirat (J75) la care sunt rotite trei cupole.
Note
[modificare | modificare sursă]- ^ a b c d e en Stephen Wolfram, "Metabigyrate rhombicosidodecahedron" from Wolfram Alpha. Retrieved February 28, 2023.
- ^ en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603




