Piramidă pătrată
| Piramidă pătrată | |
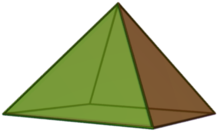 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J1 – J2 |
| Fețe | 5 (4 triunghiuri; 1 pătrat) |
| Laturi (muchii) | 8 |
| Vârfuri | 5 |
| χ | 2 |
| Configurația vârfului | 34, 4(32.4) |
| Simbol Schläfli | ( ) ∨ {4} |
| Grup de simetrie | C4v, [4], (*44), ordin 8 |
| Volum | ; (a = latura bazei) |
| Poliedru dual | autodual |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie o piramidă pătrată este o piramidă care are baza un pătrat. Dacă apexul este situat perpendicular deasupra centrului pătratului, este o piramidă pătrată dreaptă și are simetria C4v. Dacă toate lungimile laturilor sunt egale, este o piramidă pătrată echilaterală,[1] care este poliedrul Johnson J1.
Piramida pătrată oblică
[modificare | modificare sursă]O piramidă pătrată oblică cu latura bazei a și înălțimea h are volumul
- .
Piramida pătrată dreaptă
[modificare | modificare sursă]Într-o piramidă pătrată dreaptă, toate laturile laterale au aceeași lungime, iar fețele, în afară de bază, sunt triunghiuri isoscele congruente.
O piramidă pătrată dreaptă cu latura bazei a și înălțimea h are aria și volumul:
- ,
- .
Lungimea laturii laterale este:
- ;
iar apotema laterală este:
- .
Unghiurile diedre sunt:
- între bază și fețele laterale:
- ;
- între două fețe laterale adiacente:
- .
Piramida pătrată echilaterală, poliedrul Johnson J1
[modificare | modificare sursă]Dacă toate laturile au aceeași lungime, atunci fețele laterale sunt triunghiuri echilaterale, iar piramida este o piramidă pătrată echilaterală, poliedru Johnson J1.
Piramida pătrată Johnson poate fi caracterizată printr-un singur parametru, lungimea laturii a.
Înălțimea h (de la mijlocul pătratului până la apex), aria A (incluzând toate cele cinci fețe) și volumul V al unei piramide pătrate echilaterale sunt:
- ,
- ,
- .
Unghiurile diedre ale piramidei pătrate echilaterale sunt:
- între bază și fețele laterale:
- .
- între două fețe laterale adiacente:
- .
Graf
[modificare | modificare sursă]O piramidă pătrată poate fi reprezentată prin graful roată W5.
Poliedre și faguri înrudiți
[modificare | modificare sursă]| Piramide regulate | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonală | Triunghiulară | Pătrată | Pentagonală | Hexagonală | Heptagonală | Octogonală | Eneagonală | Decagonală... |
| Improprie | Regulată | Echilaterale | Isoscele | |||||

|

|

|

| |||||

|

|

|

|

|

|

|

|

|
|

|
|
|---|---|---|
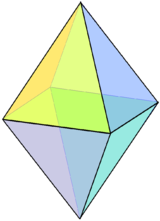
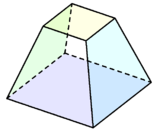
| Un octaedru regulat poate fi considerat o bipiramidă pătrată, adică două piramide pătrate Johnson conectate între ele la baze. | hexaedrul tetrakis poate fi construit dintr-un cub cu piramide pătrate scurte adăugate pe fiecare față. | Un trunchi pătrat este o piramidă pătrată cu vârful trunchiat. |
Piramidele pătrate umplu spațiul împreună cu tetraedre, cuburi trunchiate sau cuboctaedre.[2]
Poliedru dual
[modificare | modificare sursă]| Dualul piramidei pătrate | Desfășurata dualului |
|---|---|

|

|
Topologic, piramida pătrată este un poliedru autodual. Lungimile laturilor dualului sunt diferite.
Note
[modificare | modificare sursă]- ^ en Franz Hocevar, Solid Geometry, 1903, p. 44
- ^ en 凸正多角面体充填一覧表 / List of Regular polygon faced convex honeycomb
Bibliografie
[modificare | modificare sursă]- en Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- en Zalgaller, Victor (). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
Legături externe
[modificare | modificare sursă] Materiale media legate de piramidă pătrată la Wikimedia Commons
Materiale media legate de piramidă pătrată la Wikimedia Commons- en Eric W. Weisstein, Square pyramid la MathWorld.
- en Eric W. Weisstein, Johnson solid la MathWorld.
- en Eric W. Weisstein, Wheel graph la MathWorld.
- en Square Pyramid -- Interactive Polyhedron Model
- en Virtual Reality Polyhedra georgehart.com: The Encyclopedia of Polyhedra (model VRML Arhivat în , la Wayback Machine.)












