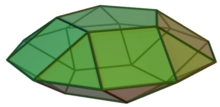
Girobicupolă pentagonală
| Girobicupolă pentagonală | |
 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J30 – J31 – J32 |
| Fețe | 22 (10 triunghiuri echilaterale, 10 pătrate), 2 pentagoane) |
| Laturi (muchii) | 40 |
| Vârfuri | 20 |
| χ | 2 |
| Configurația vârfului | 10 (3.4.3.4); 10 (3.4.5.4) |
| Grup de simetrie | D5h, [5,2], (*225), ordin 20 |
| Arie | ≈ 17,771 a2 (a = latura) |
| Volum | ≈ 4,648 a3 (a = latura) |
| Poliedru dual | Trapezoedru pentagonal alungit |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie girobicupola pentagonală este un poliedru convex construit prin unirea a două cupole pentagonale (J5) prin bazele lor decagonale, printr-o rotire de 36° a uneia dintre cele două cupole în jurul axei sale de simetrie, astfel încât fețele adiacente ale celor două cupole să fie de tip diferit. Este a treia din șirul infinit de girobicupole. Este poliedrul Johnson J31. Nu este tranzitivă pe vârfuri.
Poliedre înrudite
[modificare | modificare sursă]Fără rotirea de 36° a uneia dintre cele două cupole înainte de unire se produce ortobicupola pentagonală (J30).
Dacă dintr-un rombicosidodecaedru se îndepărtează partea de mijloc în formă de rombicosidodecaedru parabidiminuat (J80) și se unesc părțile rămase, se obține o girobicupolă pentagonală.
Dacă între cele două cupole pentagonale se inserează o prismă decagonală regulată, se obține girobicupola pentagonală alungită (J39).
Mărimi asociate
[modificare | modificare sursă]Următoarele formule pentru arie A și volum V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Note
[modificare | modificare sursă]- ^ en Stephen Wolfram, "Pentagonal+gyrobicupola Pentagonal gyrobicupola" la Wolfram Alpha, accesat 2010-07-24


