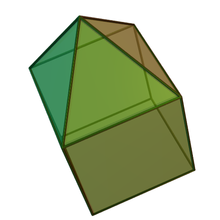
Piramidă pătrată alungită

Piramidă pătrată alungită
(model 3D)
Descriere
Tip	poliedru Johnson J7 – J8 – J9
Fețe	9 (4 triunghiuri echilaterale,     5 pătrate)
Laturi (muchii)	16
Vârfuri	9
χ	2
Configurația vârfului	1 (34); 4 (32.42); 4 (43)
Grup de simetrie	C4v, [4], (*44), ordin 8
Arie	≈ 6,732 a2   (a = latura)
Volum	≈ 1,236 a3   (a = latura)
Poliedru dual	autodual
Proprietăți	convexă
Desfășurată

În geometrie piramida pătrată alungită este un poliedru convex construit prin alungirea unei piramide pătrate prin atașarea unui cub la baza acestuia. Este poliedrul Johnson (J₈ ). Având 9 fețe, este un eneaedru.

Ca orice piramidă alungită, poliedrul rezultat este autodual din punct de vedere topologic, dar nu și din punct de vedere geometric.

Mărimi asociate

Următoarele formule pentru înălțime h, arie A și volum V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

$h=\left(1+{\frac {\sqrt {2}}{2}}\right)a\approx 1,707107\,a\,,$

$A=\left(5+{\sqrt {3}}\right)a^{2}\approx 6,732051\,a^{2},$

$V=\left(1+{\frac {\sqrt {2}}{6}}\right)a^{3}\approx 1,235702\,a^{3}.$

Dacă laturile nu au aceeași lungime, se calculează separat mărimile corespunzătoare piramidei și cubului și se adună.

Poliedre și faguri înrudiți

Piramide alungite

Piramidă digonală alungită	Piramidă triunghiulară alungită	Piramidă pătrată alungită	Piramidă pentagonală alungită	Piramidă hexagonală alungită	Piramidă heptagonală alungită	...	Con alungit

Poliedru dual

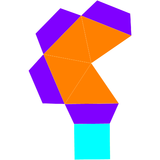
Topologic, piramida pătrată alungită este propriul său dual. Din punct de vedere geometric, dualul are nouă fețe neregulate: un pătrat, patru trapeze isoscele și patru triunghiuri isoscele.

Dualul piramidei pătrate alungite	Desfășurata dualului

Faguri

Piramida pătrată alungită poate tesela spațiul împreună cu tetraedre, similar cu fagurele tetraedric-octaedric.

Legături externe

• en Eric W. Weisstein, Elongated square pyramid la MathWorld.
• en Eric W. Weisstein, Johnson solid la MathWorld.